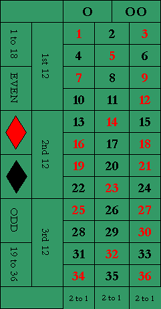
To calculate the payout of a single number bet on the European layout, you should know that the roulette table odds are 36 to 1. You should take away 1 from 36 to get 35, which is the payout rate. In a winning case scenario of a £10 single bet, you would win £350 (£10 x 35). Does the Zero have the lowest odds in roulette? From my experience, the easiest way to work out probabilities in roulette is to look at the fraction of numbers for your desired probability, then convert to a percentage or ratio from there. For example, lets say you want to know the probability of the result being red on a European wheel. Originally, I developed this app for me. The app computes automatically all the probabilities of the roulette, increases the probabilities to win, helps to design a bet strategy, and it is completely customizable. All the calculations are based on the probability theory, in the same way that professionals obtain profits. To calculate the payout of a single number bet on the European layout, you should know that the roulette table odds are 36 to 1. You should take away 1 from 36 to get 35, which is the payout rate. In a winning case scenario of a £10 single bet, you would win £350 (£10 x 35). Does the Zero have the lowest odds in roulette?
- Details
In any case, such skills require lots of time and knowledge. Alternatively, a player should have a brilliant mind. Not every player is able to calculate the odds of hitting the target. It is not so easy to calculate which the sequence of cards will be on the table. Still, many players believe the theory of probability works and can influence the course of a roulette session. In this article, we are going to consider the main roulette probability problems.
Frankly speaking, it is impossible to predict how the ball will behave in roulette. Intuition and inner voice are the only things that can guide the player. There are no other forces that can help in the struggle against a roulette ball. Why? Everything is rather clear. The player should track and remember each move during the whole session. And if players were able to do this, then casinos would immediately go bankrupt.
Yet, players seek new ways to submit a roulette ball and tame it. Many players calculate odds using the theory of probability. Below, let’s find out whether it is reasonable.
The Concept of Probability in the Game
To begin with, let’s recall what the probability theory is. The notion studies random events. The concept arose as a science from the belief that certain patterns lie at the heart of random mass events. The notion studies these patterns. The probability theory deals with the study of events, the occurrence of which is not known for sure. It allows judging the degree of probability of occurrence of some events in comparison with others.
For example, it is impossible to determine unambiguously the result of getting 'heads' or 'tails' as a result of a coin toss. Yet, with repeated tossing, approximately the same number of 'heads' and 'tails' comes up. It means that the probability that 'heads' or 'tails' drop out is equal to 50%.
A test, in this case, is the implementation of a certain set of conditions. That is, in this case, tossing a coin. The challenge can be played an unlimited number of times. In this case, the complex of conditions includes random factors. An event is the result of the test. The event happens:
- Real (always happens as a result of a test)
- Unreal (never happens)
- Accidental (may or may not happen as a result of the test)
For example, when a coin is tossed, an impossible event is that the coin will be on the edge; a random event is 'heads' or 'tails'. The particular test result is called an atomic event. As a result of the test, only elementary events occur. The collection of all possible, different, specific test outcomes is called the space of elementary events.
Probability is the degree to which an event may occur. When the grounds for some possible event outweigh the opposite grounds, then the event is called probable, otherwise unlikely, or improbable.
The same rule applies to roulette. Many players try to predict the outcome of a roulette spin with the help of the concept. Let's study this point on an example and find out what happens when using the formula. No, we are to calculate the probability of getting 5 simple odds in a row (for instance, 5 BLACK in a row).
Do not forget that a roulette ball lacks any memory. Thus, there are 5 independent events. Divide 18 by 37 to find out the probability of each of them. We get 0.49. Multiply 0.49 five times to find out the probability of a series of 5 BLACK. We get 0.03. As you see, odds are rather small. So, you need to play against such a probability to win. But how to play? Bet on RED five times? Keep in mind that the probability of five RED has no difference. The result will be the same.
Okay, let's wait for a series of four shots on BLACK, and then put on RED. Do not forget that the probability of 5 BLACK in a row is very small. We spin the roulette and finally see 4 BLACK. Now, the moment has come when you need to bet on RED. Yet, the probability of getting RED hasn't changed, as the ball lacks any experience.
Now, I would like to draw a clear analogy. Let’s say you want to pull clothes out of a wardrobe with your eyes closed. Moreover, the wardrobe is directly roulette. There are a lot of clothes in it. Your eyes are shut. When you stick your hand up a pile of clothes, you cannot know which one you will get out.
No matter how hard you try, the chances of finding the desired garment are small. But still, there are few of them. For example, you know the material by touch and perhaps remember the approximate arrangement of things in the wardrobe. Therefore, it can be said that there are certain changes, but they are small.
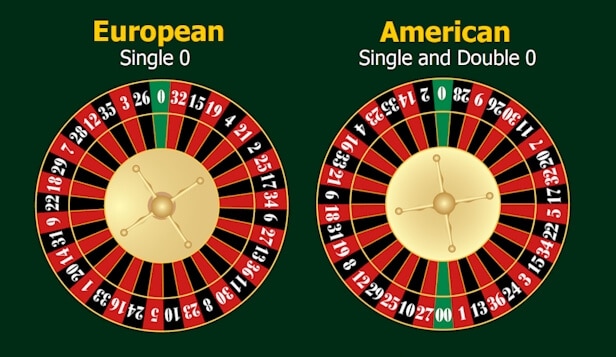
An interesting fact is the following. Odds in American roulette are estimated at 5.26%. The same indicator is 2.7% in European roulette. The difference is due to the fact that the first one has two Zeros. Actually, roulette is purely a game of luck. The gambler has odds either to win or to lose.
Precise Analysis of a Roulette Session
Let's start with the fact that in the probability theory, the concept of probability is formalized as a numerical characteristic of an event. Recall once again that it is a probabilistic measure that takes a value from 0 to 1. Value 1 corresponds to a reliable/real event. An impossible/unreal event has a probability of 0. If the probability of an event occurring is x, then the probability of its non-occurrence is 1 – x.

Let’s apply the theory to roulette. As a real event, we take the fact that the ball will stop at any number. In other words, the probability that any number will play is 1. In our case, an unreal event means that no numbers have been played. Theoretically, this is possible if the ball flies out of the wheel, or an electronic roulette freezes. Yet, in this case, the casino usually returns bets, and this happens quite rarely.
Since there are 37 numbers on the wheel and each of them can appear with the same probability, the probability of a particular number being drawn is 1/37. One should add the corresponding probabilities to determine the probability that one of several numbers will play. For example, the probability of hitting a split or one of two specific numbers is 2/37. For equal chances, the probability of falling out will be 18/37.
Use the formula 1 - 1/37 to calculate the probability that a specific number won’t play. We get that the probability of not drawing a specific number is 36/37. Still, non-hitting a number means that any of the remaining 36 numbers will play in any case. The probability of this event is just 36/37. As you can see, everything is logical.
Having calculated roulette probabilities per spin, it is interesting to look further. To calculate the probability of the same number drawing, one should multiply the corresponding probabilities. Thus, the probability that the same specific number will play twice is calculated using the formula (1/37)*(1/37). By analogy, the repetition probability for equal chances is calculated by (18/37)*(18/37). For another repetition, simply add a new multiplier. So, the likelihood of an equal chance for three times is (18/37)*(18/37)*(18/37), etc.
And finally, if the chosen number does not play during the first spin. How to calculate the probability of getting the number on the second, third, etc. spin? No way! The probability is always the same and does not depend on all previous spins. For any number, the probability of falling out is always 1/37. For an equal chance, the indicator is 18/37.
Yet, every one counts and somehow shows that with each next spin the probability of getting a specific number is constantly increasing... Here is the trick — in fact, each roulette probability chart shows the probability with which the required bet will drop out at least once during the specified number of spins.
To calculate this probability, you’re welcome to use a roulette odds calculator. It calculates the probability of not hitting the desired number in a row for a certain number of spins. The opposite of this value will be the required probability. Let’s examine this rule using the following instances.
The first one is the following: find out the probability that a particular number will appear at least once in 5 spins.
- Players’ odds of hitting a number is 1/37 or 0.027;
- The probability of missing a number is 1-1/37 = 36/37;
- The odds of not hitting a specific number 5 times in a row is (36/37) * (36/37) * (36/37) * (36/37) * (36/37) or if shorter than (36/37)^5. Numerically, it will be 0.8719;
- Thus, the probability that a specific number will not play 5 times in a row is 0.8719. The probability that the required number will play at least once in 5 spins is 1-0.8719 = 0.1281.
Let's proceed to another one: calculate the probability that RED will drop out at least once in 5 spins.
- The probability that RED drops out is 18/37 or 0.4864;
- The probability of missing RED is 1-18/37 = 19/37;
- The probability of not hitting of RED 5 times in a row is (19/37)^5 = 0.0357;
- The probability that RED will play at least once in 5 spins is 1-0.0357 = 0.9643;
- The final touch. Ordinary people are not used to dealing with a roulette probability distribution. They easier perceive information in the form of percentages. Therefore, we take the value of 100% as a real event; an impossible event corresponds to 0%. Thus, to convert to percentages, it is enough to multiply the obtained probabilities by 100.
Things to Remember Before Sitting at a Roulette Table
It is worth mentioning that an attempt to find a correct winning combination or strategy for playing roulette always fails. Remember how the story of a successful combination of cards in Pushkin's “Queen of Spades” ended. Try not to repeat such mistakes, and do not hope for a miracle.
With such a strategy, you can only change dispersion. Still, you cannot influence the mathematical expectation. Players spend much time to develop the right working strategy. Yet, keep in mind that the more bets you make, the fewer chances to win at least something in a casino you have. This rule is applied to online casinos as well.
Just think for yourself the following fact. When you visit a casino, all players and the system itself hope to get as much benefit from you as possible. Thus, you are playing the game not only according to the theory of probability and against it. You also compete with the casino itself, which is practically a separate organism. It craves benefits and large profits, which appear only in case of your loss.
If you play in an online casino, then you play against a program that is a set of letters and numbers. Simply put, your main competitor is a code.
A computer is a machine that has no intelligence, even artificial. Yet, players who expect you to fail do have intelligence. Remember that everyone starting from the owner of the casino up to its employees and visitors can’t wait to see your losses. Players should leave as much money as possible there. Then a disappointed player comes back for revenge with another big sum in a pocket. It has always been this way, and it is now.
The machine does not think and does not know how to do this. So, it simply executes commands. In other words, it carries out the programmed line code. No one needs to write any variations or tricky combinations. There is no need to create traps in the program. Simplicity and triviality are important for any computer program.
All computers in the world, no matter what they are (old or new, simple or advanced, for work or home), are equipped with random number generators. It is this generator that is considered the very heart of the computer. These generators are exactly the same. They don't have any trickery.
How to Increase Roulette Winning Odds
Every player dreams of increasing roulette odds of winning. To play roulette, you do not need to have any special knowledge. It all depends on chance. Yet, despite this fact, each player thinks about the way to increase the odds of winning the game. Thus, consider the following points to improve your odds.
- 1. It is worth paying attention to the type of roulette. Each roulette wheel has various odds of winning due to a different number of slots. For example, it is much easier to win in European roulette than in American one. Since European roulette leaves the casino with an advantage of only 2.7%, and American roulette has 5.3%.
- 2. Play on proven systems. Players are divided into 2 types: those who play relying only on their minds, and those who play according to different systems. Surely, it is more profitable to play by systems. But, in this case, choose only approved algorithms. For example, Martingale, Lucky 7, etc.
- 3. Use bonuses. Do not neglect the bonuses that a casino offers. When using them, you also increase your odds of winning. Before playing at any casino, look at a few more options and choose the one in which the wagering coefficient is minimal.
- 4. Bankroll management. If you want to win frequently, you need to follow Bankroll Management. Its essence is as follows: you need to learn how to choose the size of bets so that you can make another 150 to 300 bets with the remaining money. This strategy will help improve the roulette odds payout.
Roulette Strategies that Help to Win
Systems for playing simple roulette odds:
- Martingale strategy
- Anti-Martingale System (Parlay Strategy)
- D’Alembert system
- Anti-D’Alembert algorithm
- Labouchere method
- Anti-Labouchere systems
- Donald's strategy with Nathanson's changes
- Fibonacci strategy
Systems for playing in the main playing field:
- System of two thirds (Law of distribution)
- Biarritz System (Makarov Strategy)
- Counter-Biarritz system
How to Win at Casino Roulette
Is it possible to win at the casino by playing roulette according to the rules of the listed strategies and systems? This is how beginners usually formulate the question, without specifying other important and significant conditions of the game. Thus, roulette odds are explained by many factors.

There is no purely mathematical roulette strategy that would allow the player to completely eliminate losses. Also, no single gambling strategy can affect the mathematical profitability of a game.
In extremely rare cases, and purely due to technical reasons, roulette wheels in certain casinos may deviate from the uniform distribution of the numbers drawn.
This phenomenon is called roulette wheel addiction. Counter-Biarritz system is designed for playing against casinos in which addictive wheel roulette has been identified. Yet, even this strategy, like all others, does not exclude the factor of luck in the game.
Every single launch of the ball is luck. The player constantly runs the risk of both winning and losing. That is why the game is called roulette.
It should be noted that all mathematical systems and strategies for playing roulette were developed by the players themselves. The main idea and advantage of using a certain strategy during the game are that the player can control it and his/her deposit.
FAQ
European Roulette Probability Calculator Worksheet
Where to play?
- If you are looking for an honest and reliable casino, Fastpay is the best place for you, 100% trust. You will enjoy over 5000 casino games and super-fast withdrawals (up to 5 minutes).
For most bets, calculating your expected value (or EV) is simple. It can become harder in games where you don’t have all the information you need to make the calculations; in games like that (such as poker or blackjack), expected value often requires a little estimation along with the hard math.
In order to make an expected value calculation, you’ll need to know four things: the probability of winning the bet, the amount you’ll win if you the bet is won, the probability of losing the bet, and the amount you’ll lose if the bet is lost. You can plug actual dollar amounts into the calculations if you want to know the expected win or loss on a particular bet (as we will do) you can just use “units” for more general calculations that cover bets of any size.
Roulette Probability
Here’s an example. Imagine you are flipping a coin with a friend. However, the payouts aren’t quite fair: you only have to bet $10 on each flip, while your friend has to bet $11. What is the expected value for you?
Well, we know that you have a 50% chance of winning, and when you win, you’ll win $11. We can multiply those numbers together to come up with a total of $5.50. We also know that you’ll lose half the time, and will lose $10 each time you lose. $10 multiplied by .5 is $5. We can then take those two figures, subtract the average loss from the average win, and find that you expect to make a profit of $0.50 on each flip. The math looks like this:
European Roulette Probability Calculator Present Value
($11 * .5) – ($10 * .5) = $0.50
European Roulette Probability Calculator Formula
This is the same math used in any EV calculation, though things can get more complicated if you have to include the possibility of winning different amounts or that the bet could push.
